1.解析モデル
 |
| 図1 初期条件における解析結果 |
サイズ :□100×100㎜ 厚み10㎜
熱伝導率λ:4.7
熱源 :□20×20㎜ 厚み1㎜ 熱伝導率λ=200/熱量:1W
固定条件 :平板底部を25℃に設定、放射、対流なしの熱伝導条件のみとする。
解析ソフト :LISA 伝熱解析モード
使用要素 :6面体1次(HEX8)
2.解析結果
分割条件を熱源サイズに合わせて、□20㎜とした場合の解析結果を図1示す。
特徴的なのは・最低温度が24.81℃と拘束温度25℃より低いことである。
3.解析結果の検討
LISAのPOSTにはメッシュの断面表示機能があるが、図1のままでは中心部にメッシュが通っていないので肝心の断面を見ることができない。
以下にメッシュを種々変えた結果を上面図と断面図で示す。
|
上面図 |
断面図 |
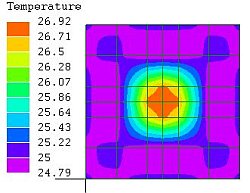
図2
基本分割図
(中心部にメッシュ追加)
24.79~
26.92℃ |
 |
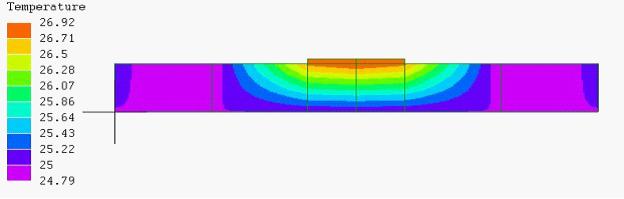 |
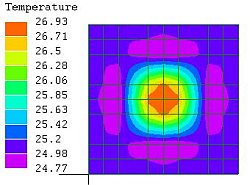
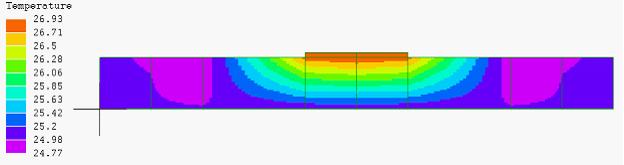
図3
周辺部のみ
細分割
24.77~
26.93℃
|
 |
 |
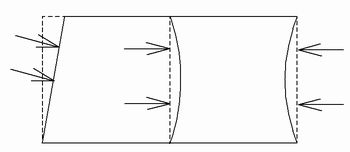 |
| 図4熱流量の移動方向 |
LISAのPOSTの断面表示機能を使うために、図2のように中心部を細分割した。結果は上面図の温度分布が図1と変わったが、分布の傾向や拘束温度より低い温度を示す現象は変わらなかった。
図3は異常を発生している周辺部を細分割したものであるが、異常現象そのものには改善がみられなかった。
(中心部はメッシュ変更なし)
図2,図3の温度分布をよく見ると、外縁の要素境界付近で縦方向に温度コンタ-の面が分布しており、熱流量が面に垂直に流れていると考えれば、図4の矢印のように模式化できる。
元々の有限要素法との対応では「力=熱流量」/「変位=温度差」であるので、応力の流れについて変形を考えてみると図4実線のように力(=熱流量)が流れている事が考えられる。即ち、この要素の蓄積エネルギーは負なのである。
つまり、温度変化を発生しているセルサイズが大きいため、積分点の値を節点へ外挿する影響が大きく出すぎて隣接セルの温度変化が負になったものと考えられる。
温度変化が発生している箇所をやはり複数個のセルに分ける必要があるのではないだろうか?
確認の為、温度分布が激しく変化している発熱体中心部近傍のセルを細分化したものを図5~7に示す。
|
上面図 |
断面図 |
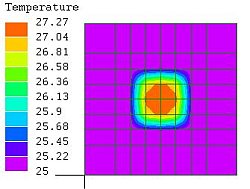
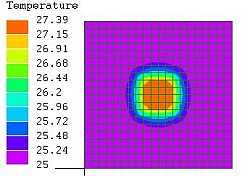
図5
中心部のみ
細分割
25~
27.27℃ |
 |
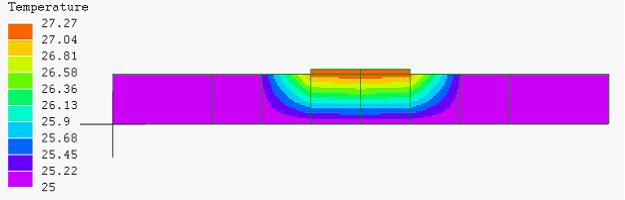 |
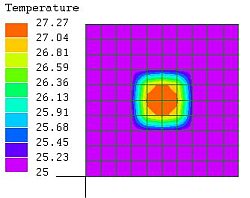
図6
全体細分割
10X10
25~
27.27℃ |
 |
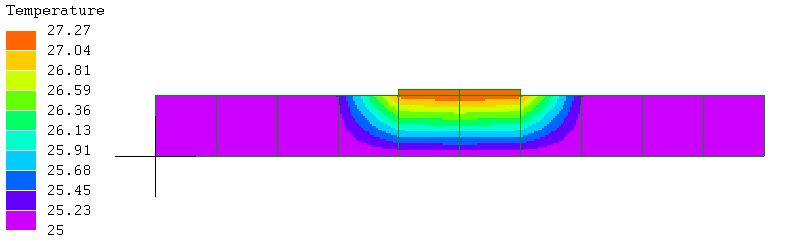 |
図7
全体4倍密度
20X20
25~
27.39℃ |
 |
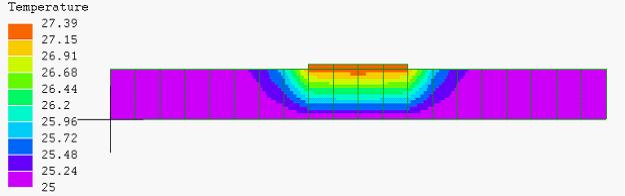 |
図5~7では温度の変化が、中心部から±20㎜で完了しており、セル幅を20ミリとした図1、2、3では現象を捉えきれていなかったことが分かる。その為、このセルの熱エネルギーを過大に評価し、隣接セルのエネルギーが負になったと考えられる。
又、同図の最高温度は27℃を超えており、明らかに図1,2、3の結果とは異なっている。
次に、要素の次数を上げた場合の事例を次に示す。
|
上面図 |
断面図 |
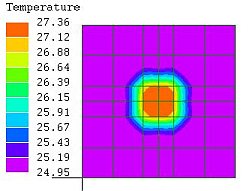
図8
図2の要素を
2次要素に変更
24.95~
27.36℃ |
 |
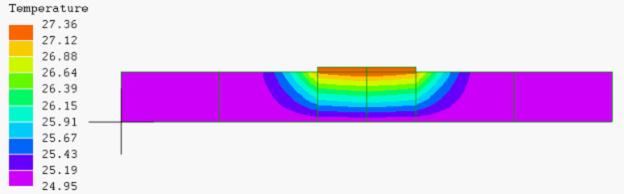 |
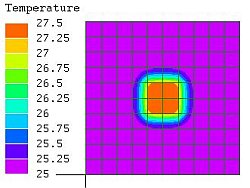
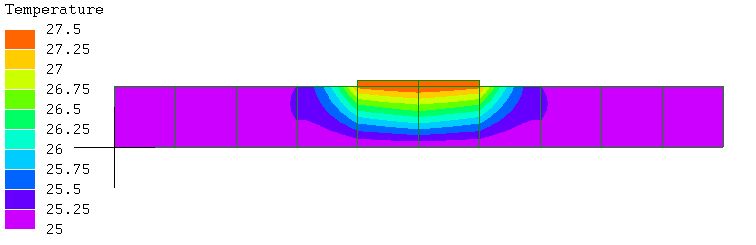
図9
図6の要素を
2次要素に変更
10X10
25~
27.5℃ |
 |
 |
2次要素にすることで図8ではかなり改善されているが上面図の温度分布がスムースではなく歪であり、不完全であることが分かる。一方、温度分布の形状はある程度、捕まえているのでメッシュの密度を裏付ける資料としては有効である。
図9のようにメッシュを細かくして温度変化を捉えきるようにしないと2次要素でも正確な温度計算はできない。ただ、2次要素特有の温度分布が高次曲面になっているのは気になる。本来、低温部の温度分布は高次曲面にはならない筈なので、1次要素でメッシュ数を上げる方が好ましいのではないだろうか?
有限体積法では面に出入りする物理量を計算するので、積分点自身を持たないし、差分法では節点自身の値を取り扱うので外挿しないからこの様な事は原理的に発生し難い。
この現象はLISA特有のものなのか、それともFEMソルバー固有のものなのかは追って検討する。 |